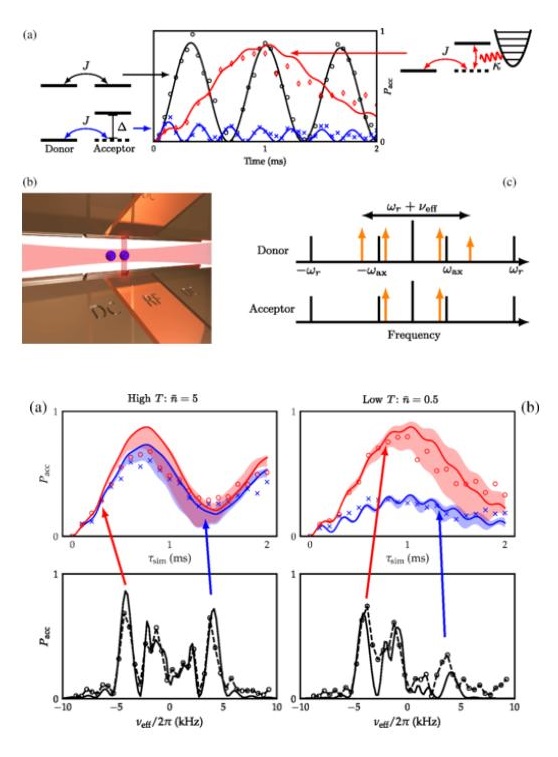
Quantum Simulation
Understanding complicated quantum-many-body dynamics is notoriously difficult leading often to numerically intractable situations. A way out of this dilemma is to engineer a well-controlled quantum system with which the quantum dynamics of interest can be implemented and thus studied in detail by changing the parameters of the quantum simulation, or better emulation. As a case study, we study charge and energy transfer models relevant to many important processes in chemistry, biology, and emerging nanotechnologies. Such transfer processes often occur in noisy thermal environments that strongly modify the transfer dynamics and, in some cases, even improve the transport efficiency or robustness. A prominent example is the energy transfer from pigments in light-harvesting complexes towards reaction centers, where efficiency is believed to critically depend on the spectral properties of the environment. In these processes, the dominant sources of fluctuations and noise are often intramolecular vibrations and solvent dynamics. Understanding the influence of this molecular environment on transport dynamics requires solving complex and often fully quantized models that become intractable to theoretical treatments even for systems of moderate size.
By implementing a minimal model, we observe vibrationally assisted energy transport between the electronic states of a donor and an acceptor ion augmented by coupling the donor ion to its vibration. We tune our emulator into several parameter regimes and, in particular, investigate the transfer dynamics in the nonperturbative regime often found in biochemical situations. In the future, we plan to study these transfer process while including more sites coupled to different engineered environmental conditions. In collaboration with Birgitta Whaley (University of California, Berkeley) and Mohan Sarovar (Sandia National Laboratories), we aim to bring new understanding to energy transduction and transport in materials, and help improve the design of new photodetectors and new photovoltaic systems.
More details can be found in:
Phys. Rev. X 8, 011038 (2018)
Verifying an analog quantum simulator
Analog quantum simulation is expected to be a significant application of near-term quantum devices. Verification of these devices without comparison to known simulation results will be an important task as the system size grows beyond the regime that can be simulated classically. We introduce a set of experimentally-motivated verification protocols for analog quantum simulators, discussing their sensitivity to a variety of error sources and their scalability to larger system sizes. We demonstrate these protocols experimentally using a two-qubit trapped-ion analog quantum simulator and numerically using models of up to five qubits.
Taken together, these techniques allow for pragmatic evaluation of an analog quantum simulation device in a way that builds confidence that the device is not only operating consistently, but that it is also operating faithfully according to the desired target Hamiltonian. Such techniques can be applied to subsets of a larger system to allow an experimentalist to characterize and diagnose the behavior in a scalable way.
More information is available at:
npj Quantum Inf. 7, 46 (2021)
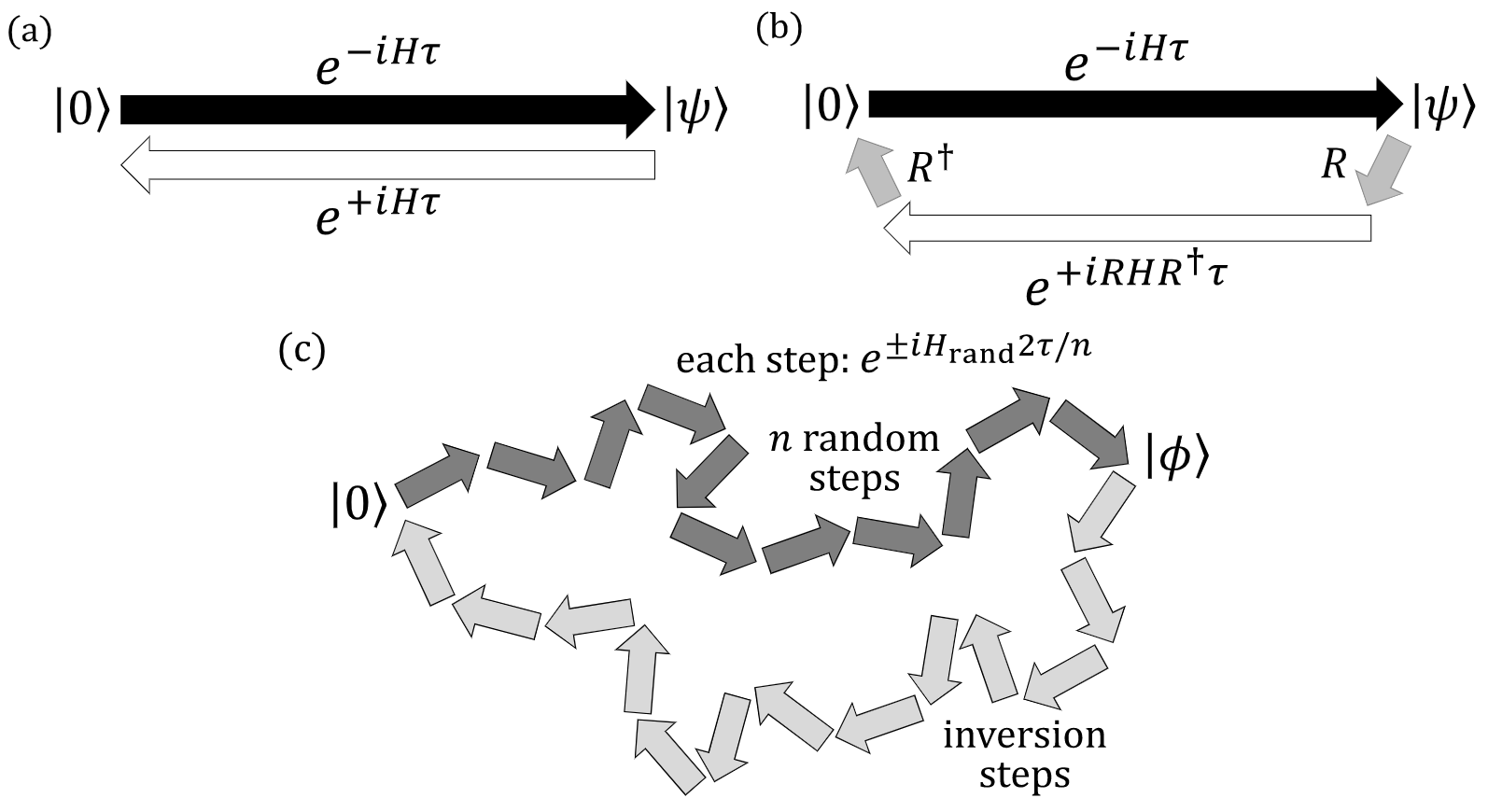
(a) Time-reversal analog verification: Running an analog simulation forward in time, followed by the same analog simulation backward in time.
(b) Multi-basis analog verification: Running an analog simulation forward in time, rotating the state, performing the backward simulation by an analog version in the rotated basis, and finally rotating the state back.
(c) Randomized analog verification: Running a random sequence of subsets of the Hamiltonian terms (denoted as Hrand), followed by an inversion sequence of subsets of the Hamiltonian terms which has been calculated to return the system approximately to a basis state.
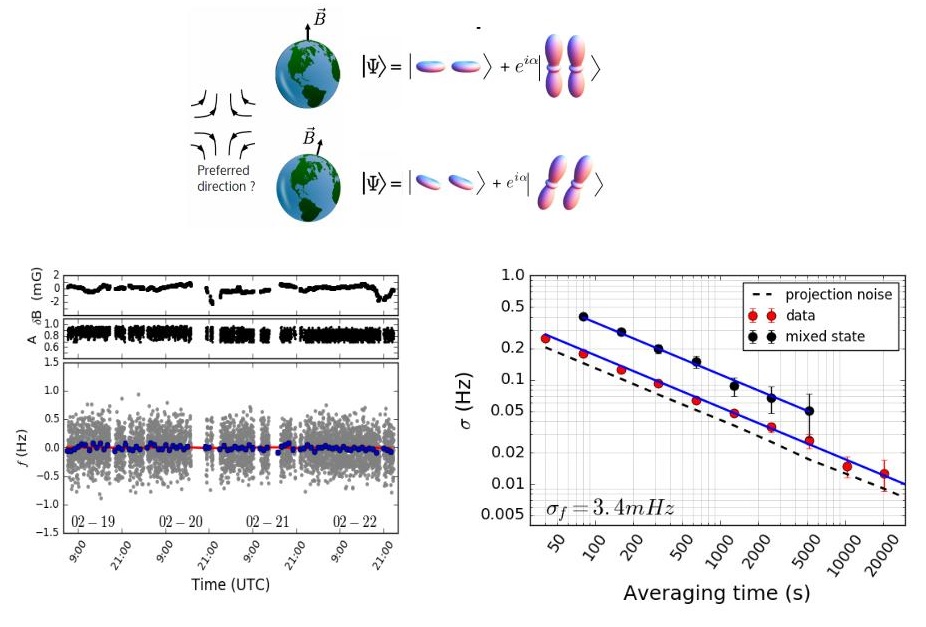
Precision measurements using trapped ions
The best-known tests for the isotropy of space are Michelson-Morley type experiments. We perform such a test not with light, but with electrons. We measure the energy difference between two orientations of the electronic wavefunction of Calcium ions. As the Earth rotates, the absolute spatial orientation of the two parts of the wave packet changes, and anisotropies in the electron dispersion will change the phase of the interference signal. Using tools borrowed from quantum information we are able to verify spatial Lorentz symmetry to a precision at the 1e-18 level and below.
In addition, we experimentally study how precision measurements can be improved by preparing entangled states immune to the dominant source of decoherence. Using calcium ions, we explicitly demonstrate the advantage from entanglement on a precision test of local Lorentz invariance for the electron. Reaching the quantum projection noise limit set by quantum mechanics, we observe for bipartite entangled states the expected gain of a factor of two in the precision. Under specific conditions, multipartite entangled states may yield substantial further improvements. Our measurements improve the previous best limit for local Lorentz invariance of the electron using calcium ions by factor of two to about 5e-19.
More details can be found in:
Nature 517, 592 (2015)
Nature Physics 12, 465-468 (2016)
Phys. Rev. Lett. 120, 103202 (2018)
Phys. Rev. Lett. 122, 123605 (2019)